blog/_posts/mathematics/measure-theory/2023-02-06-measurable-functions.md

share, toc, math, categories, path, tags, title, date, github_title, image, attachment

share	toc	math	categories	path	tags	title	date	github_title	image	attachment
true	true	true	Mathematics Measure Theory	_posts/mathematics/measure-theory	math analysis measure-theory	04. Measurable Functions	2023-02-06	2023-02-06-measurable-functions	path /assets/img/posts/mathematics/measure-theory/mt-04.png	folder assets/img/posts/mathematics/measure-theory

Lebesgue integral을 공부하기 전 마지막 준비입니다. Lebesgue integral은 다음과 같이 표기합니다.

\int _ X f \,d{\mu}

표기를 보면 크게 3가지 요소가 있음을 확인할 수 있습니다. 바로 집합 X, measure \mu, 그리고 함수 $f$입니다. 집합과 measure는 다루었으니 마지막으로 함수에 관한 이야기를 조금 하면 Lebesgue integral을 정의할 수 있습니다!

Measurable Function

이제부터 다루는 measurable function 관련 내용은 일반적인 measurable space $(X, \mathscr{F})$에서 논의합니다. 여기서 $\mathscr{F}$는 당연히 $\sigma$-algebra on $X$입니다.

정의. (Measurable Function) Measurable space $(X, \mathscr{F})$와 함수 f : X \rightarrow\overline{\mathbb{R}} 가 주어졌을 때, 모든 a \in \mathbb{R} 에 대하여 집합

\lbrace x \in X : f(x) > a\rbrace

가 measurable이면 $f$를 measurable function이라 한다.¹

위 사실로부터 다음을 바로 알 수 있습니다.

따름정리. $\mathbb{R}^p$에서 정의된 연속함수는 Lebesgue measurable이다.

증명. 임의의 a \in \mathbb{R} 에 대해 $\lbrace x : f(x) > a\rbrace$가 $\mathbb{R}^p$의 열린집합이므로, $\mathfrak{M}(m)$의 원소가 되어 measurable이다.

위 정의를 보고 생각하다 보면 굳이 f(x) > a 로 정의해야 했나 의문이 생깁니다. f(x) \geq a, f(x) < a 를 사용할 수도 있었을 것입니다.

정리. Measurable space X 위에서 정의된 함수 $f$가 주어졌을 때, 다음은 동치이다.

1. 모든 a \in \mathbb{R} 에 대하여 $\lbrace x : f(x) > a\rbrace$는 measurable이다.

2. 모든 a \in \mathbb{R} 에 대하여 $\lbrace x : f(x) \geq a\rbrace$는 measurable이다.

3. 모든 a \in \mathbb{R} 에 대하여 $\lbrace x : f(x) < a\rbrace$는 measurable이다.

4. 모든 a \in \mathbb{R} 에 대하여 $\lbrace x : f(x) \leq a\rbrace$는 measurable이다.

증명. 우선 (1)을 가정하고, 다음 관계식을 이용하면

\begin{aligned} \lbrace x : f(x) \geq a\rbrace & = f^{-1}\left( [a, \infty) \right) \\ & = f^{-1}\left( \bigcup _ {n=1}^{\infty} \left( a + \frac{1}{n}, \infty \right) \right) \\ & = \bigcup _ {n=1}^{\infty} f^{-1}\left( \left( a + \frac{1}{n}, \infty \right) \right) \end{aligned}

measurable set의 countable union도 measurable이므로 ($\sigma$-algebra) (2)가 성립한다. 이제 (2)를 가정하면

\lbrace x : f(x) < a\rbrace = X \setminus\lbrace x : f(x) \geq a\rbrace

로부터 (3)이 성립하는 것을 알 수 있다. (3)을 가정하면 위와 마찬가지 방법으로

\begin{aligned} \lbrace x : f(x) \leq a\rbrace & = f^{-1}\left( (-\infty, a] \right) \\ & = f^{-1}\left( \bigcup _ {n=1}^{\infty} \left( -\infty, a - \frac{1}{n} \right) \right) \\ & = \bigcup _ {n=1}^{\infty} f^{-1}\left( \left( -\infty, a - \frac{1}{n} \right) \right) \end{aligned}

과 같이 변형하여 (4)가 성립함을 알 수 있다. 마지막으로 (4)를 가정하면

\lbrace x : f(x) > a\rbrace = X \setminus\lbrace x : f(x) \leq a\rbrace

로부터 (1)이 성립함을 알 수 있다.

Properties of Measurable Functions

이제 정의를 살펴봤으니, measurable function들이 어떠한 성질을 갖는지 살펴봅니다.

정리. $f$가 measurable이면 $\lvert f \rvert$도 measurable이다.

증명. 다음 관계로부터 자명하다.

\lbrace x : \lvert f(x) \rvert < a\rbrace = \lbrace x : f(x) < a\rbrace \cap \lbrace x : f(x) > -a\rbrace.

역은 성립할까요?

참고. 역은 성립하지 않는다. Measurable하지 않은 S \subseteq(0, \infty) 위에서 함수 $g$를 다음과 같이 정의하자.

g(x) = \begin{cases} x & (x \in S) \\ -x & (x \notin S). \end{cases}

그러면 모든 x \in \mathbb{R} 에 대해 \lvert g(x) \rvert = x 이므로 $\lvert g \rvert$는 measurable function이다. 하지만 \lbrace x : g(x) > 0\rbrace = \mathbb{R}\setminus(-\infty, 0] = S 는 measurable이 아니므로 $g$는 measurable function이 아니다.

명제. $f, g$가 measurable function이라 하자.

1. \max\lbrace f, g\rbrace, $\min\lbrace f, g\rbrace$는 measurable function이다.

2. f^+ = \max\lbrace f, 0\rbrace, f^- = -\min\lbrace f, 0\rbrace 는 measurable function이다.

증명. 다음과 같이 적는다.

\begin{aligned} \lbrace x : \max\lbrace f, g\rbrace > a\rbrace & = \lbrace x : f(x) > a\rbrace \cup \lbrace x : g(x) > a\rbrace \\ \lbrace x : \min\lbrace f, g\rbrace < a\rbrace & = \lbrace x : f(x) < a\rbrace \cup \lbrace x : g(x) < a\rbrace \end{aligned}

그리고 (2)는 (1)에 의해 자명하다.

다음은 함수열의 경우입니다. Measurable 함수열의 극한함수도 measurable일까요?

정리. $\lbrace f _ n\rbrace$가 measurable 함수열이라 하자. 그러면

\sup _ {n\in \mathbb{N}} f _ n, \quad \inf _ {n\in \mathbb{N}} f _ n, \quad \limsup _ {n \rightarrow\infty} f _ n, \quad \liminf _ {n \rightarrow\infty} f _ n

은 모두 measurable이다.

증명. 다음이 성립한다.

\inf f _ n = -\sup\left( -f _ n \right), \quad \limsup f _ n = \inf _ n \sup _ {k\geq n} f _ k, \quad \liminf f _ n = -\limsup\left( -f _ n \right).

따라서 위 명제는 $\sup f _ n$에 대해서만 보이면 충분하다. 이제 $\sup f _ n$이 measurable function인 것은

\lbrace x : \sup _ {n\in\mathbb{N}} f _ n(x) > a\rbrace = \bigcup _ {n=1}^{\infty} \lbrace x : f _ n(x) > a\rbrace \in \mathscr{F}

로부터 당연하다.

$\lim f _ n$이 존재하는 경우, 위 명제를 이용하면 \lim f _ n = \limsup f _ n = \liminf f _ n 이기 때문에 다음을 알 수 있습니다. Measurability는 극한에 의해서 보존됩니다!

따름정리. 수렴하는 measurable 함수열의 극한함수는 measurable이다.

이제 마지막으로 measurable 함수의 합과 곱 또한 measurable이면 좋겠습니다. 각각 증명하는 것도 방법이지만, 두 경우를 한꺼번에 증명할 수 있는 방법이 있습니다.

정리. $X$에서 정의된 실함수 $f, g$가 measurable이라 하자. 연속함수 F: \mathbb{R}^2 \rightarrow\mathbb{R} 에 대하여 h(x) = F\big(f(x), g(x)\big) 는 measurable이다. 이로부터 $f + g$와 $fg$가 measurable임을 알 수 있다.²

증명. a \in \mathbb{R} 에 대하여 G _ a = \lbrace (u, v)\in \mathbb{R}^2 : F(u, v) > a\rbrace 로 정의합니다. 그러면 $F$가 연속이므로 $G _ a$는 열린집합이고, G _ a 열린구간의 합집합으로 적을 수 있다. 따라서 a _ n, b _ n, c _ n, d _ n\in \mathbb{R} 에 대하여

G _ a = \displaystyle\bigcup _ {n=1}^{\infty} (a _ n, b _ n) \times (c _ n, d _ n)

로 두면

\begin{aligned} \lbrace x \in X : F\bigl(f(x), g(x)\bigr) > a\rbrace = & \lbrace x \in X : \bigl(f(x), g(x)\bigr) \in G _ a\rbrace \\ = & \bigcup _ {n=1}^{\infty} \lbrace x \in X : a _ n < f(x) < b _ n,\, c _ n < g(x) < d _ n\rbrace \\ = & \bigcup _ {n=1}^{\infty} \lbrace x \in X : a _ n < f(x) < b _ n\rbrace \cap \lbrace x \in X : c _ n < g(x) < d _ n\rbrace \end{aligned}

이다. 여기서 $f, g$가 measurable이므로 $\lbrace x \in X : F\bigl(f(x), g(x)\bigr) > a\rbrace$도 measurable이다. 이로부터 F(x, y) = x + y, F(x, y) = xy 인 경우를 고려하면 f+g, $fg$가 measurable임을 알 수 있다.

Characteristic Function

아래 내용은 Lebesgue integral의 정의에서 사용할 매우 중요한 building block입니다.

정의. (Characteristic Function) 집합 E \subseteq X 의 characteristic function $\chi _ E$는 다음과 같이 정의한다.

\chi _ E(x) = \begin{cases} 1 & (x\in E) \\ 0 & (x \notin E). \end{cases}

참고로 characteristic function은 indicator function 등으로도 불리며, $\mathbf{1} _ E, K _ E$로 표기하는 경우도 있습니다.

Simple Function

정의. (Simple Function) 함수 s: X\rightarrow\mathbb{R} 의 치역이 유한집합이면 simple function이라 한다.

치역이 유한집합임을 이용하면 simple function은 다음과 같이 적을 수 있습니다.

참고. 치역의 원소를 잡아 s(X) = \lbrace c _ 1, c _ 2, \dots, c _ n\rbrace 로 두자. 여기서 E _ i = s^{-1}(c _ i) 로 두면 다음과 같이 적을 수 있다.

s(x) = \sum _ {i=1}^{n} c _ i \chi _ {E _ i}(x).

이로부터 모든 simple function은 characteristic function의 linear combination으로 표현됨을 알 수 있습니다. 물론 $E _ i$는 쌍마다 서로소입니다.

여기서 $E _ i$에 measurable 조건이 추가되면, 정의에 의해 $\chi _ {E _ i}$도 measurable function입니다. 따라서 모든 measurable simple function을 measurable $\chi _ {E _ i}$의 linear combination으로 표현할 수 있습니다.

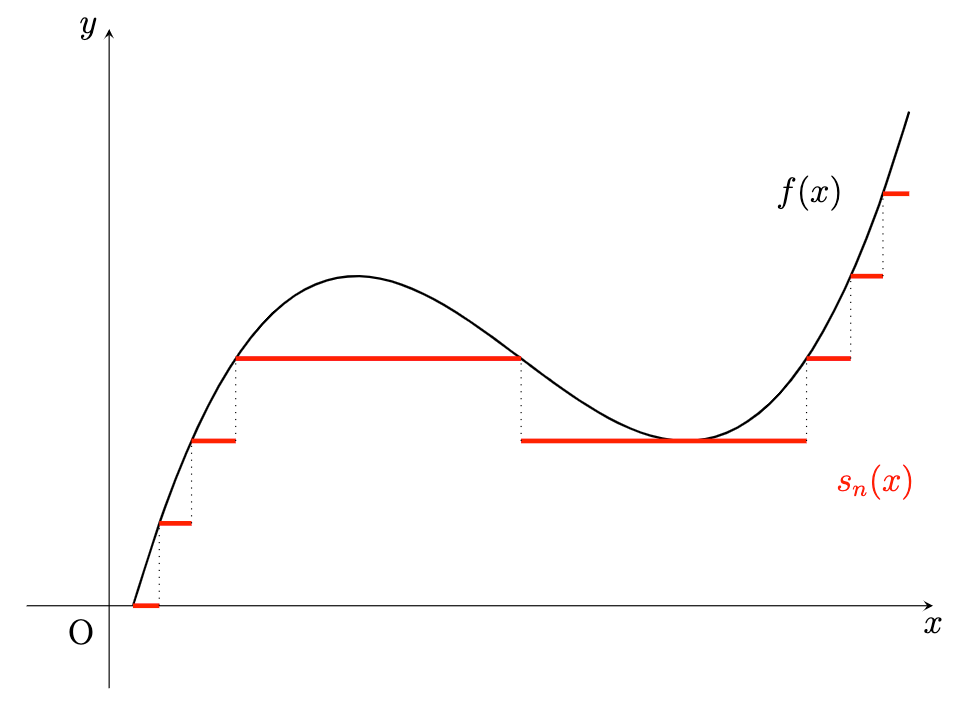
아래 정리는 simple function이 Lebesgue integral의 building block이 되는 이유를 잘 드러냅니다. 모든 함수는 simple function으로 근사할 수 있습니다.

정리. f : X \rightarrow\overline{\mathbb{R}} 라 두자. 모든 x \in X 에 대하여

\lim _ {n \rightarrow\infty} s _ n(x) = f(x), \quad \lvert s _ n(x) \rvert \leq \lvert f(x) \rvert

인 simple 함수열 $s _ n$이 존재한다. 여기서 추가로

1. $f$가 유계이면 $s _ n$은 $f$로 고르게 수렴한다.

2. f\geq 0 이면 단조증가하는 함수열 $s _ n$이 존재하며 \displaystyle\sup _ {n\in \mathbb{N}} s _ n = f 이다.

3. $f$가 measurable이면 measurable simple 함수열 $s _ n$이 존재한다.

증명. 우선 f \geq 0 인 경우부터 보인다. n \in \mathbb{N} 에 대하여 집합 $E _ {n, i}$를 다음과 같이 정의한다.

E _ {n, i} = \begin{cases} \left\lbrace x : \dfrac{i}{2^n} \leq f(x) < \dfrac{i+1}{2^n}\right\rbrace & (i = 0, 1, \dots, n\cdot 2^n - 1) \\ \lbrace x : f(x) \geq n\rbrace & (i = n\cdot 2^n) \end{cases}

이를 이용하여

s _ n(x) = \sum _ {n=0}^{n\cdot 2^n} \frac{i}{2^n} \chi _ {E _ {n, i}} (x)

로 두면 $s _ n$은 simple function이다. 여기서 $E _ {n, i}$와 $s _ n$의 정의로부터 s _ n(x) \leq f(x) 은 자연스럽게 얻어지고, x \in \lbrace x : f(x) < n\rbrace 에 대하여 \lvert f(x) - s _ n(x) \rvert \leq 2^{-n} 인 것도 알 수 있다. 여기서 f(x) \rightarrow\infty 로 발산하는 부분이 존재하더라도, 충분히 큰 $n$에 대하여 \lbrace x : f(x) \geq n\rbrace 위에서는 s _ n(x) = n \rightarrow\infty 이므로 문제가 되지 않는다. 따라서

\lim _ {n \rightarrow\infty} s _ n(x) = f(x), \quad (x \in X)

라 할 수 있다.

(1)을 증명하기 위해 $f$가 유계임을 가정하면, 적당한 M > 0 에 대해 f(x) < M 이다. 그러면 충분히 큰 $n$에 대하여 \lbrace x : f(x) < n\rbrace = X 이므로 모든 x \in X 에 대해

\lvert f(x) - s _ n(x) \rvert \leq 2^{-n}

가 되어 $s _ n$이 $f$로 고르게 수렴함을 알 수 있다.

(2)의 경우 $s _ n$의 정의에 의해 단조증가함을 알 수 있다. 여기서 f \geq 0 조건은 분명히 필요하다. s _ n(x) \leq s _ {n+1}(x) 이므로 당연히 \displaystyle\sup _ {n\in \mathbb{N}} s _ n = f 이다.

(3)을 증명하기 위해 $f$가 measurable임을 가정하면 $E _ {n, i}$도 measurable이므로 $s _ n$은 measurable simple 함수열이 된다.

이제 일반적인 $f$에 대해서는 f = f^+ - f^- 로 적는다.³ 그러면 앞서 증명한 사실을 이용해 g _ n \rightarrow f^+, h _ n \rightarrow f^- 인 simple function $g _ n, h _ n$을 잡을 수 있다. 이제 s _ n = g _ n - h _ n 으로 두면 \lvert s _ n(x) \rvert \leq \lvert f(x) \rvert 가 성립하고, s _ n \rightarrow f 도 성립한다.

한편 이 정리를 이용하면 f + g, $fg$가 measurable임을 증명하기 쉬워집니다. 단, f+g, $fg$가 잘 정의되어야 합니다. 이는 \infty - \infty 와 같은 상황이 발생하지 않는 경우를 말합니다.

따름정리. $f, g$가 measurable이고 f + g, $fg$가 잘 정의된다면, $f+g$와 $fg$는 measurable이다.

증명. $f, g$를 각각 measurable simple function $f _ n, g _ n$으로 근사한다. 그러면

f _ n + g _ n \rightarrow f + g, \quad f _ ng _ n \rightarrow fg

이고 measurability는 극한에 의해 보존되므로 $f+g, fg$는 measurable이다.

---

1. 일반적으로는 ‘measurable set의 preimage가 measurable이 될 때’로 정의합니다. ↩︎

2. 참고로 \infty - \infty 의 경우는 정의되지 않으므로 생각하지 않습니다. ↩︎

3. 이 정의에서 \infty - \infty 가 나타나지 않음에 유의해야 합니다. ↩︎