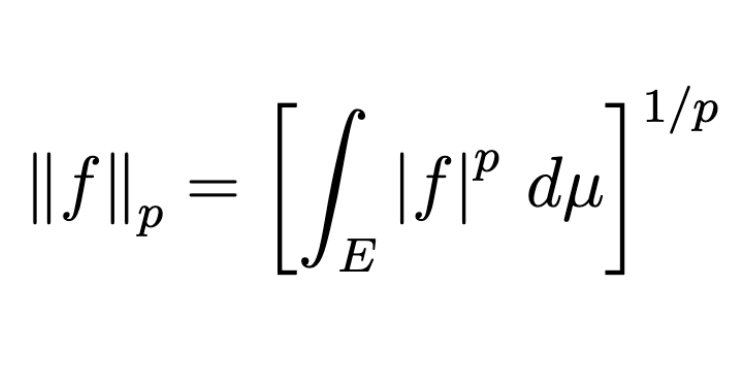blog/_posts/Mathematics/Measure Theory/2023-07-31-Lp-functions.md

share, toc, math, categories, tags, title, date, github_title, image

share	toc	math	categories	tags	title	date	github_title	image
true	true	true	Mathematics Measure Theory	math analysis measure-theory	09. $\mathcal{L}^p$ Functions	2023-07-31	2023-07-31-Lp-functions	path /assets/img/posts/mt-09.png

{: .w-50}

Integration on Complex Valued Function

Let (X, \mathscr{F}, \mu) be a measure space, and E \in \mathscr{F}.

정의.

1. A complex valued function f = u + iv, (where u, v are real functions) is measurable if u and v are both measurable.

2. For a complex function f,

   f \in \mathcal{L}^{1}(E, \mu) \iff \int_E \left\lvert f \right\rvert \,d{\mu} < \infty \iff u, v \in \mathcal{L}^{1}(E, \mu).

3. If f = u + iv \in \mathcal{L}^{1}(E, \mu), we define

   \int_E f \,d{\mu} = \int_E u \,d{\mu} + i\int_E v \,d{\mu}.

참고.

1. Linearity also holds for complex valued functions. For f_1, f_2 \in \mathcal{L}^{1}(\mu) and \alpha \in \mathbb{C},

   \int_E \left( f_1 + \alpha f_2 \right) \,d{\mu} = \int_E f_1 \,d{\mu} + \alpha \int_E f_2 \,d{\mu}.

2. Choose c \in \mathbb{C} and \left\lvert c \right\rvert = 1 such that \displaystyle c \int_E f \,d{\mu} \geq 0. This is possible since multiplying by c is equivalent to a rotation.

Now set cf = u + vi where u, v are real functions and the integral of v over E is 0. Then,

\begin{aligned} \left\lvert \int_E f \,d{\mu} \right\rvert & = c \int_E f\,d{\mu} = \int_E u \,d{\mu} \\ & \leq \int_E (u^2+v^2)^{1/2} \,d{\mu} \\ & = \int_E \left\lvert cf \right\rvert \,d{\mu} = \int_E \left\lvert f \right\rvert \,d{\mu}. \end{aligned}

Functions of Class \mathcal{L}^{p}

\mathcal{L}^p Space

Assume that (X, \mathscr{F}, \mu) is given and X = E.

정의. (\mathcal{L}^{p}) A complex function f is in \mathcal{L}^{p}(\mu) if f is measurable and \displaystyle\int_E \left\lvert f \right\rvert ^p \,d{\mu} < \infty.

정의. ($\mathcal{L}^{p}$-norm) $\mathcal{L}^{p}$-norm of f is defined as

\left\lVert f \right\rVert_p = \left[\int_E \left\lvert f \right\rvert ^p \,d{\mu} \right]^{1/p}.

Inequalities

정리. (Young Inequality) For a, b \geq 0, if p > 1 and 1/p + 1/q = 1, then

ab \leq \frac{a^p}{p} + \frac{b^q}{q}.

증명. From 1/p + 1/q = 1, p - 1 = \frac{1}{q - 1}. The graph y = x^{p - 1} is equal to the graph of x = y^{q - 1}. Sketch the graph on the $xy$-plane and consider the area bounded by x = 0, x = a, y = 0, y = b. Then we directly see that

\int_0^a x^{p-1} \,d{x} + \int_0^b y^{q-1} \,d{y} \geq ab,

with equality when a^p = b^q. Evaluating the integral gives the desired inequality.

참고. For $\mathscr{F}$-measurable f, g on X,

\left\lvert fg \right\rvert \leq \frac{\left\lvert f \right\rvert ^p}{p} + \frac{\left\lvert g \right\rvert ^q}{q} \implies \left\lVert fg \right\rVert_1 \leq \frac{\left\lVert f \right\rVert_p^p}{p} + \frac{\left\lVert g \right\rVert_q^q}{q}

by Young inequality. In particular, if \left\lVert f \right\rVert_p = \left\lVert g \right\rVert_q = 1, then \left\lVert fg \right\rVert_1 \leq 1.

정리. (Hölder Inequality) Let 1 < p < \infty and \displaystyle\frac{1}{p} + \frac{1}{q} = 1. If f, g are measurable,

\left\lVert fg \right\rVert_1 \leq \left\lVert f \right\rVert_p \left\lVert g \right\rVert_q.

So if f \in \mathcal{L}^{p}(\mu) and g \in \mathcal{L}^{q}(\mu), then fg \in \mathcal{L}^{1}(\mu).

증명. If \left\lVert f \right\rVert_p = 0 or \left\lVert g \right\rVert_q = 0 then f = 0 a.e. or g = 0 a.e. So fg = 0 a.e. and \left\lVert fg \right\rVert_1 = 0.

Now suppose that \left\lVert f \right\rVert_p > 0 and \left\lVert g \right\rVert_q > 0. By the remark above, the result directly follows from

\left\lVert \frac{f}{\left\lVert f \right\rVert_p} \cdot \frac{g}{\left\lVert g \right\rVert_q} \right\rVert_1 \leq 1.

정리. (Minkowski Inequality) For 1 \leq p < \infty, if f, g are measurable, then

\left\lVert f + g \right\rVert_p \leq \left\lVert f \right\rVert_p + \left\lVert g \right\rVert_p.

증명. If f, g \notin \mathcal{L}^{p}, the right hand side is \infty and we are done. For p = 1, the equality is equivalent to the triangle inequality. Also if \left\lVert f + g \right\rVert_p = 0, the inequality holds trivially. We suppose that p > 1, f, g \in \mathcal{L}^p and \left\lVert f+g \right\rVert_p > 0.

Let q = \frac{p}{p-1}. Since

\begin{aligned} \left\lvert f + g \right\rvert ^p & = \left\lvert f + g \right\rvert \cdot \left\lvert f + g \right\rvert ^{p - 1} \\ & \leq \bigl(\left\lvert f \right\rvert + \left\lvert g \right\rvert \bigr) \left\lvert f + g \right\rvert ^{p-1}, \end{aligned}

we have

\begin{aligned} \int \left\lvert f+g \right\rvert ^p & \leq \int \left\lvert f \right\rvert \cdot \left\lvert f+g \right\rvert ^{p-1} + \int \left\lvert g \right\rvert \cdot \left\lvert f+g \right\rvert ^{p-1} \\ & \leq \left( \int \left\lvert f \right\rvert ^p \right)^{1/p}\left( \int \left\lvert f+g \right\rvert ^{(p-1)q} \right)^{1/q} \\ & \quad + \left( \int \left\lvert q \right\rvert ^p \right)^{1/p}\left( \int \left\lvert f+g \right\rvert ^{(p-1)q} \right)^{1/q} \\ & = \left( \left\lVert f \right\rVert_p + \left\lVert g \right\rVert_p \right) \left( \int \left\lvert f+g \right\rvert ^p \right)^{1/q}. \end{aligned}

Since \left\lVert f + g \right\rVert_p^p > 0, we have

\begin{aligned} \left\lVert f + g \right\rVert_p & = \left( \int \left\lvert f+g \right\rvert ^p \right)^{1/p} \\ & = \left( \int \left\lvert f+g \right\rvert ^p \right)^{1 - \frac{1}{q}} \\ & \leq \left\lVert f \right\rVert_p + \left\lVert g \right\rVert_p. \end{aligned}

정의. f \sim g \iff f = g $\mu$-a.e. and define

[f] = \left\lbrace g : f \sim g\right\rbrace.

We treat [f] as an element in \mathcal{L}^{p}(X, \mu), and write f = [f].

참고.

1. We write \left\lVert f \right\rVert_p = 0 \iff f = [0] = 0 in the sense that f = 0 $\mu$-a.e.

2. Now \lVert \cdot \rVert_p is a norm in \mathcal{L}^{p}(X, \mu) so d(f, g) = \left\lVert f - g \right\rVert_p is a metric in \mathcal{L}^{p}(X, \mu).

Completeness of \mathcal{L}^p

Now we have a function space, so we are interested in its completeness.

정의. (Convergence in \mathcal{L}^p) Let f, f_n \in \mathcal{L}^{p}(\mu).

1. f_n \rightarrow f in \mathcal{L}^p(\mu) \iff \left\lVert f_n-f \right\rVert_p \rightarrow 0 as n \rightarrow\infty.

2. \left( f_n \right)_{n=1}^\infty is a Cauchy sequence in \mathcal{L}^{p}(\mu) if and only if

\forall \epsilon > 0, \exists\,N > 0 such that n, m \geq N \implies \left\lVert f_n-f_m \right\rVert_p < \epsilon.

도움정리. Let \left( g_n \right) be a sequence of measurable functions. Then,

\left\lVert \sum_{n=1}^{\infty} \left\lvert g_n \right\rvert \right\rVert_p \leq \sum_{n=1}^{\infty} \left\lVert g_n \right\rVert_p.

Thus, if \displaystyle\sum_{n=1}^{\infty} \left\lVert g_n \right\rVert_p < \infty, then \displaystyle\sum_{n=1}^{\infty} \left\lvert g_n \right\rvert < \infty $\mu$-a.e. So \displaystyle\sum_{n=1}^{\infty} g_n < \infty $\mu$-a.e.

증명. By monotone convergence theorem and Minkowski inequality,

\begin{aligned} \left\lVert \sum_{n=1}^{\infty} \left\lvert g_n \right\rvert \right\rVert_p & = \lim_{m \rightarrow\infty} \left\lVert \sum_{n=1}^{m} \left\lvert g_n \right\rvert \right\rVert_p \\ & \leq \lim_{n \rightarrow\infty} \sum_{n=1}^{m} \left\lVert g_n \right\rVert_p \\ & = \sum_{n=1}^{\infty} \left\lVert g_n \right\rVert_p < \infty. \end{aligned}

Thus \displaystyle\sum_{n=1}^{\infty} \left\lvert g_n \right\rvert < \infty $\mu$-a.e. and \displaystyle\sum_{n=1}^{\infty} g_n < \infty $\mu$-a.e. by absolute convergence.

정리. (Fischer) Suppose \left( f_n \right) is a Cauchy sequence in \mathcal{L}^{p}(\mu). Then there exists f \in \mathcal{L}^{p}(\mu) such that f_n \rightarrow f in \mathcal{L}^{p}(\mu).

증명. We construct \left( n_k \right) by the following procedure.

\exists\,n_1 \in \mathbb{N} such that \left\lVert f_m - f_{n_1} \right\rVert_p < \frac{1}{2} for all m \geq n_1.

\exists\,n_2 \in \mathbb{N} such that \left\lVert f_m - f_{n_2} \right\rVert_p < \frac{1}{2^2} for all m \geq n_2.

Then, \exists\,1 \leq n_1 < n_2 < \cdots < n_k such that \left\lVert f_m - f_{n_k} \right\rVert_p < \frac{1}{2^k} for m \geq n_k.

Since \displaystyle\left\lVert f_{n_{k+1}} - f_{n_k} \right\rVert_p < \frac{1}{2^k}, we have

\sum_{k=1}^{\infty} \left\lVert f_{n_{k+1}} - f_{n_k} \right\rVert_p < \infty.

By the above lemma, \sum \left\lvert f_{n_{k+1}} - f_{n_k} \right\rvert and \sum (f_{n_{k+1}} - f_{n_k}) are finite. Let f_{n_0} \equiv 0. Then as m \rightarrow\infty,

f_{n_{m+1}} = \sum_{k=0}^{m} \left( f_{n_{k+1}} - f_{n_k} \right)

converges $\mu$-a.e. Take N \in \mathscr{F} with \mu(N) = 0 such that f_{n_k} converges on X \setminus N. Let

f(x) = \begin{cases} \displaystyle\lim_{k \rightarrow\infty} f_{n_k} (x) & (x \in X \setminus N) \\ 0 & (x\in N) \end{cases}

then f is measurable. Using the convergence,

\begin{aligned} \left\lVert f - f_{n_m} \right\rVert_p & = \left\lVert \sum_{k=m}^{\infty} \left( f_{n_{k+1}} (x) - f_{n_k}(x) \right) \right\rVert_p \\ & \leq \left\lVert \sum_{k=m}^{\infty} \left\lvert f_{n_{k+1}} (x) - f_{n_k}(x) \right\rvert \right\rVert_p \\ & \leq \sum_{k=m}^{\infty} \left\lVert f_{n_{k+1}} - f_{n_k} \right\rVert_p \leq 2^{-m} \end{aligned}

by the choice of f_{n_k}. So f_{n_k} \rightarrow f in \mathcal{L}^{p}(\mu). Also, f = (f - f_{n_k}) + f_{n_k} \in \mathcal{L}^{p}(\mu).

Let \epsilon > 0 be given. Since \left( f_n \right) is a Cauchy sequence in \mathcal{L}^{p}, \exists\,N \in \mathbb{N} such that for all n, m \geq N, \left\lVert f_n - f_m \right\rVert < \frac{\epsilon}{2}. Note that n_k \geq k, so n_k \geq N if k \geq N. Choose N_1 \geq N such that for k \geq N, \left\lVert f - f_{n_k} \right\rVert_p < \frac{\epsilon}{2}. Then for all k \geq N_1,

\left\lVert f - f_k \right\rVert_p \leq \left\lVert f - f_{n_k} \right\rVert_p + \left\lVert f_{n_k} - f_k \right\rVert_p < \frac{\epsilon}{2} + \frac{\epsilon}{2} = \epsilon.

참고. \mathcal{L}^{p} is a complete normed vector space, also known as Banach space.

정리. C[a, b] is a dense subset of \mathcal{L}^{p}[a, b]. That is, for every f \in \mathcal{L}^{p}[a, b] and \epsilon > 0, \exists\,g \in C[a, b] such that \left\lVert f - g \right\rVert_p < \epsilon.

증명. Let A be a closed subset in [a, b], and consider a distance function

d(x, A) = \inf_{y\in A} \left\lvert x - y \right\rvert , \quad x \in [a, b].

Since d(x, A) \leq \left\lvert x - z \right\rvert \leq \left\lvert x - y \right\rvert + \left\lvert y - z \right\rvert for all z \in A, taking infimum over z \in A gives d(x, A) \leq \left\lvert x - y \right\rvert + d(y, A). So

\left\lvert d(x, A) - d(y, A) \right\rvert \leq \left\lvert x - y \right\rvert ,

and d(x, A) is continuous. If d(x, A) = 0, \exists\,x_n \in A such that \left\lvert x_n - x \right\rvert \rightarrow d(x, A) = 0. Since A is closed, x \in A. We know that x \in A \iff d(x, A) = 0.

Let

g_n(x) = \frac{1}{1 + n d(x, A)}.

g_n is continuous, g_n(x) = 1 if and only if x \in A. Also for all x \in [a, b] \setminus A, g_n(x) \rightarrow 0 as n \rightarrow\infty. By Lebesgue’s dominated convergence theorem,

\begin{aligned} \left\lVert g_n - \chi_A \right\rVert_p^p & = \int_A \left\lvert g_n - \chi_A \right\rvert ^p \,d{x} + \int_{[a, b]\setminus A} \left\lvert g_n - \chi_A \right\rvert ^p \,d{x} \\ & = 0 + \int_{[a, b]\setminus A} \left\lvert g_n \right\rvert ^p \,d{x} \rightarrow 0 \end{aligned}

since \left\lvert g_n \right\rvert ^p \leq 1. We have shown that characteristic functions of closed sets can be approximated by continuous functions in \mathcal{L}^{p}[a, b].

For every A \in \mathfrak{M}(m), \exists\,F_\text{closed} \subseteq A such that m(A \setminus F) < \epsilon. Since \chi_A - \chi_F = \chi_{A \setminus F},

\begin{aligned} \int \left\lvert \chi_A-\chi_F \right\rvert ^p \,d{x} & = \int \left\lvert \chi_{A\setminus F} \right\rvert ^p \,d{x} \\ & = \int_{A\setminus F} \,d{x} = m(A \setminus F) < \epsilon. \end{aligned}

Therefore, for every A \in \mathfrak{M}, \exists\,g_n \in C[a, b] such that \left\lVert g_n - \chi_A \right\rVert_p \rightarrow 0 as n \rightarrow\infty. So characteristic functions of any measurable set can be approximated by continuous functions in \mathcal{L}^{p}[a, b].

Next, for any measurable simple function f = \sum_{k=1}^{m}a_k \chi_{A_k}, we can find g_n^k \in C[a, b] so that

\left\lVert f - \sum_{k=1}^{m} a_k g_n^k \right\rVert_p = \left\lVert \sum_{k=1}^{m}a_k \left( \chi_{A_k} - g_n^k \right) \right\rVert_p \rightarrow 0.

Next for f \in \mathcal{L}^{p} and f \geq 0, there exist simple functions f_n \geq 0 such that f_n \nearrow f in \mathcal{L}^{p}. Finally, any f \in \mathcal{L}^{p} can be written as f = f^+ - f^-, which completes the proof.

이러한 확장을 몇 번 해보면 굉장히 routine합니다. \chi_F for closed F \rightarrow \chi_A for measurable A \rightarrow measurable simple f \rightarrow 0\leq f \in \mathcal{L}^{p} \rightarrow f \in \mathcal{L}^{p} 와 같은 순서로 확장합니다.